0. Úvod a provokativní čísla

Svůj článek o diferenciálním počtu jsem rozčlenil do několika kapitol. V každé z nich se diskutuje o jednom uzavřeném problému více či méně z reálného života, za to však vždy neobvyklého. Pro řešení tohoto problému potřebujeme vybudovat nové matematické nástroje, což tvoří hlavní smysl příslušné kapitoly. Celá série pak směřuje k poetické fundamentální větě diferenciálního počtu, která na předchozí články posvítí novým světlem a otevře spoustu nových perspektiv v problémech z fysiky. V celé sérii nepředpokládám žádné přílišné matematické znalosti, takže vysvětlení snad může pochopit každý. Matematická neznalost snad může být i výhodou, neboť člověk nové myšlenky může přijmout a nemusí se trápit s předchozími miskoncepcemi.
Na konci série pak jako dodatek nad rámec předpokládaných znalostí přikládám odvození derivací a integrálů některých funkcí (vysvětlím, o co jde) spolu s přehlednou tabulkou.

Co je to diferenciální počet?

Anglický fysik Isaac Newton přišel v 17. století s tzv. zákonem síly (2. Newtonovým zákonem), kterým vysvětloval pohyb těles. Podle něj se tělesa pohybují díky silám, které tělesům udělují zrychlení. Znamená to tedy, že pokud zapůsobíme silou o velikosti $F$ na těleso o hmotnosti $m$, tak těleso dostane zrychlení $a=F/m$. Zrychlení např. $100\,\mathrm{m/s}^2$ při tom znamená, že za jednu sekundu se tělesu zvýší rychlost o $100\,\mathrm{m/s}$. Ve škole se pak každý může dozvědět, že pokud má těleso nějaké zrychlení, tak lze jednoduše spočítat, jakou dráhu urazí v čase.

Tímto by se většinou příběh o Newtonovi uzavřel, nicméně buďme trochu všeteční. Co se stane když síla, která působí na nějaké těleso, se nějak mění? Např. když parašutista padá s padákem, tehdy na padák tlačí vzduch, který jej zpomaluje. Jenže samozřejmě čím pomaleji padá, tím pomaleji vzduch do padáku naráží, a tedy se zmenšuje brzdná síla. Čím rychleji padá, tím více zpomaluje, ale tím pomaleji padá a tím méně zpomaluje... Cože, dává to smysl? Nebo si představme raketu Saturn V vylétávající z atmosféry. Tato raketa, jež vynesla r. 1968 muže na Měsíc, spalovala 20 tun paliva za sekundu a palivo tvořilo 85 procent její hmotnosti. Každý ví, že čím je něco lehčí, tím lépe to zrychluje, tedy Saturn V s každou sekundou zrychloval víc a víc, ale jak přesně?

Diferenciální počet dokáže vysvětlit např. výše zmíněné děje a ještě mnohem víc. Někdy se mu též říká infinitesimální počet, neboť pro zkoumání dějů využívá infinitesimální (tj. nekonečně malé) veličiny, pracuje s nekonečny. Pro diferenciální počet je typická následující otázka: „Co bylo dřív, průměrná rychlost nebo okamžitá rychlost? Tj. je (z matematického hlediska) jednodušší říci, že z Prahy do Brna jsem jel průměrně stovkou, nebo že právě na kole jedu čtyřicítkou?“ Většina lidí by řekla, že jednodušší je okamžitá rychlost, nicméně chyba lávky. Tradičně zavádíme nejprve průměrnou rychlost jako celkovou vzdálenost uraženou za celkový čas a okamžitá rychlost je jen průměrná rychlost měřená přes nekonečně malý čas.

Seznámení se s diferenciálním počtem vyžaduje jednak trochu trpělivosti, za druhé však otevřenou mysl. Některé věci, které při cestě potkáme se totiž zdají kontraintuitivní a možná se budete zdráhat je přijmout. Jako ukázku ošemetnosti při zacházení s nekonečny se budeme ve zbytku kapitoly věnovat různým druhům čísel, v příští kapitole se pak vrhneme na něco, co již více souvisí s tématem. Držme se na naší cestě hesla: kdyby to bylo přímočaré, nebylo by to tak zajímavé!

Kolik je přirozených čísel?

Často počítáme věci na prstech: 1, 2, 3,... Čísla, která k tomu používáme, matematici nazývají přirozená (neobsahují nulu). Těmito přirozenými čísly můžeme jednoduše popsat, kolik něčeho je. Máme např. pytel brambor a můžeme říci, že v něm je 21 brambor. Nebo že včera spadlých kapek deště je 210 929 293, či by šel vyjádřit počet zrnek písku na pláži. Co kdybychom ale dali všechny přirozená čísla do pytle (např. bychom je napsali na papír), kolik by jich tam bylo?

Řekněme, že čísla do pytle dáváme popořadě. Potom, kdybychom chtěli říci, že jich je tam třeba 1 000, tak nejvyšší číslo by bylo 1 000, zapomněli jsme na 1 001! Přidali bychom ho, ale zase je opomenuté 1 002. A tak pořád dále. Tedy počet přirozených čísel v pytli nelze popsat žádným číslem. Chce se říci, že jich je tam nekonečno, ale protože čtete text o diferenciálním počtu, popíšeme toto nekonečno detailněji. Matematici by řekli, že pytel přirozených čísel je množina, a že počet čísel v ní je její mohutnost. Tak například množina čísel $\{ 1;\, 2;\, 3\}$ je množina čísel obsahující čísla 1, 2 a 3 a její mohutnost je 3, neboť obsahuje 3 prvky. Množinu přirozených čísel nazýváme $\mathbb{N}$ (pozměněné písmeno N) a její mohutnost není žádné číslo, místo toho ji nazýváme $\aleph_0$ (alef nula; alef je první písmeno hebrejské abecedy).

Mohutnost přirozených čísel jsme sice pojmenovali, ale nic jsme se tím o ní nedozvěděli. Zkusme ji porovnat s mohutností jiných množin. Vězměme například množinu sudých přirozených čísel, do které patří 2, 4, 6, 8, 10... Obě množiny jsou sice nekonečné, nicméně porovnat je mezi sebou lze. Počínejme si jako bačové, kteří chtějí spočítat dvě stáda ovcí. Ovcí je mnoho a těžko se v nich lze vyznat. Můžeme ale vždy k ovci z jednoho stáda přiřadit ovci z druhého stáda a obě je poslat pryč. Pokud se nám podaří takto všechny ovce spárovat, tak je jich v obou stádech stejně. Pokud ale např. v prvním stádu všechny ovce přiřadíme k ovcím z druhého stáda a ve druhém stádě ještě nějaké zbydou, pak je druhé stádo větší.

To je úžasné, neboť tento způsob by šel aplikovat i na nekonečné množiny. Zkusme tedy dvě zmíněné množiny porovnat jako bačové. Máme tak množinu $\mathbb{N}$, v níž jsou čísla. Nějaké číslo z té množiny pojmenujeme $n$. Druhou množinu sudých čísel pojmenujme $2\mathbb{N}$ a nějaké číslo z této množiny $m$. Nejprve přiřaďme ovce z $\mathbb{N}$ k ovcím z $2\mathbb{N}$. Ke každému číslu $n$, které nás může napadnout, vybereme číslo $m=2n$ ze sudé množiny. Přiřadili jsme tedy ke každému číslu z $\mathbb{N}$ jedinečné číslo z $2\mathbb{N}$ jako na obrázku níže.

Nyní zkusme opačné přiřazení: z $2\mathbb{N}$ do $\mathbb{N}$. Každému číslu $m$ dejme číslo $n=m/2$. Číslo $m$ je sudé, takže $m/2$ vskutku patří do $\mathbb{N}$. Tímto způsobem dostane zase každé číslo z $2\mathbb{N}$ jedinečné číslo z $\mathbb{N}$. Přiřazení si můžeme představit jako nákres výše jen s obrácenými šipkami.

Dokázali jsme tedy dvě studované množiny jedna ku jedné spárovat. To ale znamená, že mají stejnou mohutnost! To může překvapit, neboť množina sudých čísel vznikne tak, že z množiny přirozených čísel odebereme lichá čísla, tedy nekonečně prvků. Přesto se ale velikost množiny nezmění, ukazuje to jen, že je nesmyslné ptát se, kolik dá nekonečno mínus nekonečno.

Stejnou velikost obou studovaných množin lze snad pochopit lépe, pokud se na jejich prvky podíváme z blízka. Co kdybychom v množině sudých čísel nepsali $\{2;\,4;\, 6;\dots \}$ ale $\{2\cdot 1;\, 2\cdot 2;\, 2\cdot 3;\, \dots \}$? Při počítání prvků je přeci jedno, jestli počítáme jedna, dvě, tři, čtyři, anebo jestli počítáme dva krát jedna, dva krát dva, dva krát tři, dva krát čtyři. Proto dává smysl, že prvků v obou množinách je stejně.

Kolik je nekonečno?

Množinám s mohutností $\aleph_0$ se říká spočetné množiny. Intuitivně to znamená to, že kdybychom měli k disposici nekonečné množství času, tak bychom dokázali vyjmenovat jejich všechny prvky. Existují ale i množiny s ještě větší mohutností než $\aleph_0$, ty se nazývají nespočetné.

Jednou z nespočetných množin je množina reálných čísel, $\mathbb{R}$. Čas od času potřebujeme něco změřit a pro tento účel reálná čísla zazáří. Bereme si k měření nějaký metr, a na něm čteme čísla jako 2,3 (centimetrů) a 6,91 (centimetrů) nebo 0,242 (milimetrů). Čísla tohoto druhu jsou reálná čísla. Do reálných čísel zahrnujeme i nulu a i záporná čísla, patří do nich i všechna přirozená čísla. Zároveň uvažujeme, že metry mohou dosahovat jakékoliv délky chceme (případně si můžeme zvolit jiné jednotky na metru), a že metr můžeme mít tak přesný, jak jen budeme chtít. Přesností myslíme to, že na metru můžeme změřit milimetry, desetiny milimetru i miliontiny milimetru atp., to znamená, že reálná čísla mohou mít libovolný počet desetinných míst a mohou být libovolně velká.

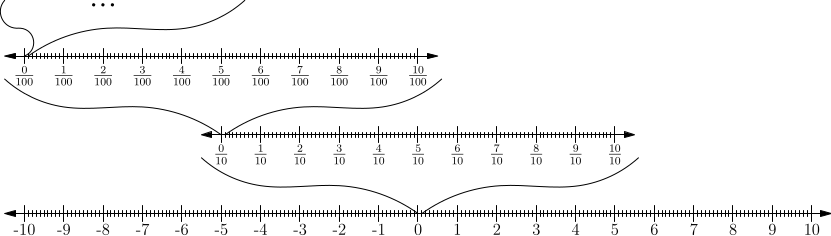
Porovnejme nyní množinu $\mathbb{N}$ a $\mathbb{R}$. Zkusme to udělat, jako vidíme na obrázku.

Zde lze vidět, že přirozených čísel je znatelně méně než reálných a ukazuje se, proč se reálným číslům říká nespočetná množina. Kdybychom totiž počítali reálná čísla od jedničky, tak ani s nekonečným časem bychom se nedostali k číslu 1,2! Tedy mohotnust reálných čísel je větší než mohutnost přirozených.

Tvrzení o mohutnosti reálných čísel by šlo dokázat matematičtěji, já však raději místo toho ukážu jinou věc. A to sice, že množina reálných čísel v intervalu od $0$ do $10$ má stejnou velikost (mohutnost) jako množina reálných čísel v intervalu od $0$ do $1$. Postup se od minulé úvahy příliš nezmění. První množinu si pojmenujeme $\mathbb{R}_{0,1}$ a druhou $\mathbb{R}_{0,10}$. Zkusíme přiřadit prvky první ke druhé: libovolné číslo $r$ z množiny $\mathbb{R}_{0,1}$ dostane přiřazené číslo $s=10\cdot r$ z $\mathbb{R}_{0,10}$.

Naopak můžeme přiřadit libovolnému prvku $s$ z množiny $\mathbb{R}_{0,10}$ jiný jednoznačný prvek $r=s/10$, který patři do množiny $\mathbb{R}_{0,1}$ (tomu odpovídá obrácení šipek na obrázku výše). Dosáhli jsme toho, že jsme vytvořili jedna ku jedné, jednoznačné párování prvků z obou množin. Za každý prvek z $\mathbb{R}_{0,1}$ máme přesně jeden prvek z množiny $\mathbb{R}_{0,10}$, a tedy mají množiny stejnou mohutnost. Opět lze množiny rozepsat jako $\{0,12;\, 0,38;\, 0,2189;\, 0,11;\dots \}$ a $\{10\cdot 0,12;\, 10\cdot 0,38;\, 10\cdot 0,2189;\, 10\cdot 0,11;\dots \}$, takže snad již jejich porovnání nepřekvapí.

Pomocí podobného triku jako výše lze ukázat, že jakýkoliv interval $\mathbb{R}$ má stejnou mohutnost jako jakýkoliv jiný interval, ba i jako samotné $\mathbb{R}$. Této mohutnosti se říká $\aleph_1$. Snad vám toto přijde zvláštní, nicméně taková vlastnost reálných čísel se hodí při popisování našeho světa. Uvažme například čas. Ten měříme pomocí reálných čísel (např. v sekundách), nicméně není žádná nejmenší časová jednotka (ani setina sekundy, ani tisícina). Požadavek, že libovolně malý okamžik se dá dělit libovolně jemně nám dává naději, protože znamená, že čas plyne spojitě, bez záškubů.

Tento nezvyklý poznatek o husté podstatě reálných čísel se mi zdá jako trefný počátek cesty za podstatou diferenciálního počtu. Ony výroky o nekonečnech vás možná překvapily, a možná jim nechcete věřit. Ať je to jak chce, jedná se o matematicky konsistentní poznatky, těžším úkolem bývá poznat, jakým způsobem souvisejí s naším reálným světem. Snad tedy následující články nabídnou vhodnou perspektivu.

>> Další kapitola