O návodu

Asymptote je mocný program, pomocí kterého lze vytvářet profesionálně vypadající vektorové obrázky, grafy či nákresy. Jedná se o jakousi „novější versi” Metapostu, kterému se velice podobá, jen je přímočařejší na použití. Pomocí Asymptote (či Metapostu) jsem vytvořil své nákresy do série článků Oživlá Geometrie. V programu lze kreslit 2D i 3D nákresy, já se budu soustředit pouze na 2D nákresy.

Podobně jako LaTeX se nejedná o WYSIWIG program ale o programovací jazyk. Obrázky kreslíte ne pomocí myši, ale tak, že programu řeknete, co chcete dostat, a on vám to vytvoří. Výhoda tohoto způsobu spočívá v tom, že můžete nakreslit přesné analytické křivky jako např. graf funkce $y=\sqrt{x}$, ale také to, že můžete recyklovat kód, který jste již napsali, či pomocí for smyček vytvářet pokročilé obrazce a ušetřit si čas.

Cílem tohoto návodu je předat velmi stručně, jak se program instaluje, a jak jej lze využít ke kreslení základních objektů a funkcí. Zaujme-li vás program, můžete si o jeho funkcích detailněji přečíst v manuálu nebo si přečíst delší anglický tutoriál.

Instalace

Začněmě tím nejtěžším – instalací programu a napsáním Hello World programu. Pokud si chcete program jen tak zkusit bez instalace, tak můžete zkusit online prostředí pro Asymptote. Abychom vytvářeli obrázky, budeme potřebovat následující tři věci:

• Program Asymptote, který vytvoří z našeho zdrojového kódu obrázky.
• Program TeXmaker, pomocí kterého budeme psát zdrojové kódy.
• Program GhostScript, abychom mohli použít formát pdf.

Program Asymptote v základu neobsahuje žádné grafické rozhraní. Vy si ho nainstalujete a on na vašem PC zůstane v pozadí. Až jej budete potřebovat, zavoláte ho, a on vám podle vašich příkazů vytvoří obrázek. Texmaker naopak potřebujeme, abychom tyto příkazy mohli napsat. Bude to naše grafické rozhraní, ve kterém napíšeme náš obrázek, a pak si jej i prohlédneme. Program GhostScript, to je jen jakási závislost, která programu Asymptote pomáhá při prác s pdf soubory.

Technické detaily

V instalace počítám s tím, že používáte operační systém Windows 10, a že máte na disku volných cca 1GB místa.

Používáte-li Linux, lze instalační kroky nahradit jediným řádkem do terminálu. Pro Ubuntu:

	sudo apt-get install asymptote texmaker ghostscript
	

Pro Arch Linux:

	sudo pacman -S asymptote texmaker ghostscript
	

• Asymptote si stáhněte zde.
• Texmaker si stáhněte zde.
• GhostScript si stáhněte zde.

První obrázek

Vytvořte si v počítači složku a v ní soubor s názvem např. hw.asy. Tento soubor otevřete v programu Texmaker. Do okna napište následující:

	settings.outformat = "pdf";
unitsize(1cm);

draw(unitsquare);
	

První řádek nám říká, že chceme použít formát pdf. Tento formát se hodí pro to, abyste si výsledek mohli nechat zobrazit v Texmakeru. Můžete ho však změnit např. na png (tím se ale ztratí vektorovost) či na svg nebo eps. Může se vám stát, že některé věci (třeba šrafování) se rozbijí pro formát svg, proto doporučuji používat pdf či eps. Může se koneckonců bez problémů vložit do .tex dokumentu.

Následně si změňte kompilátor na program Asymptote jako na obrázku vedle tlačítka nahoře s šipkou. Nyní když na šipku kliknete nebo zmáčknete F1, soubor se zkompiluje (přeloží) a na pravé straně uvidíte výsledek.

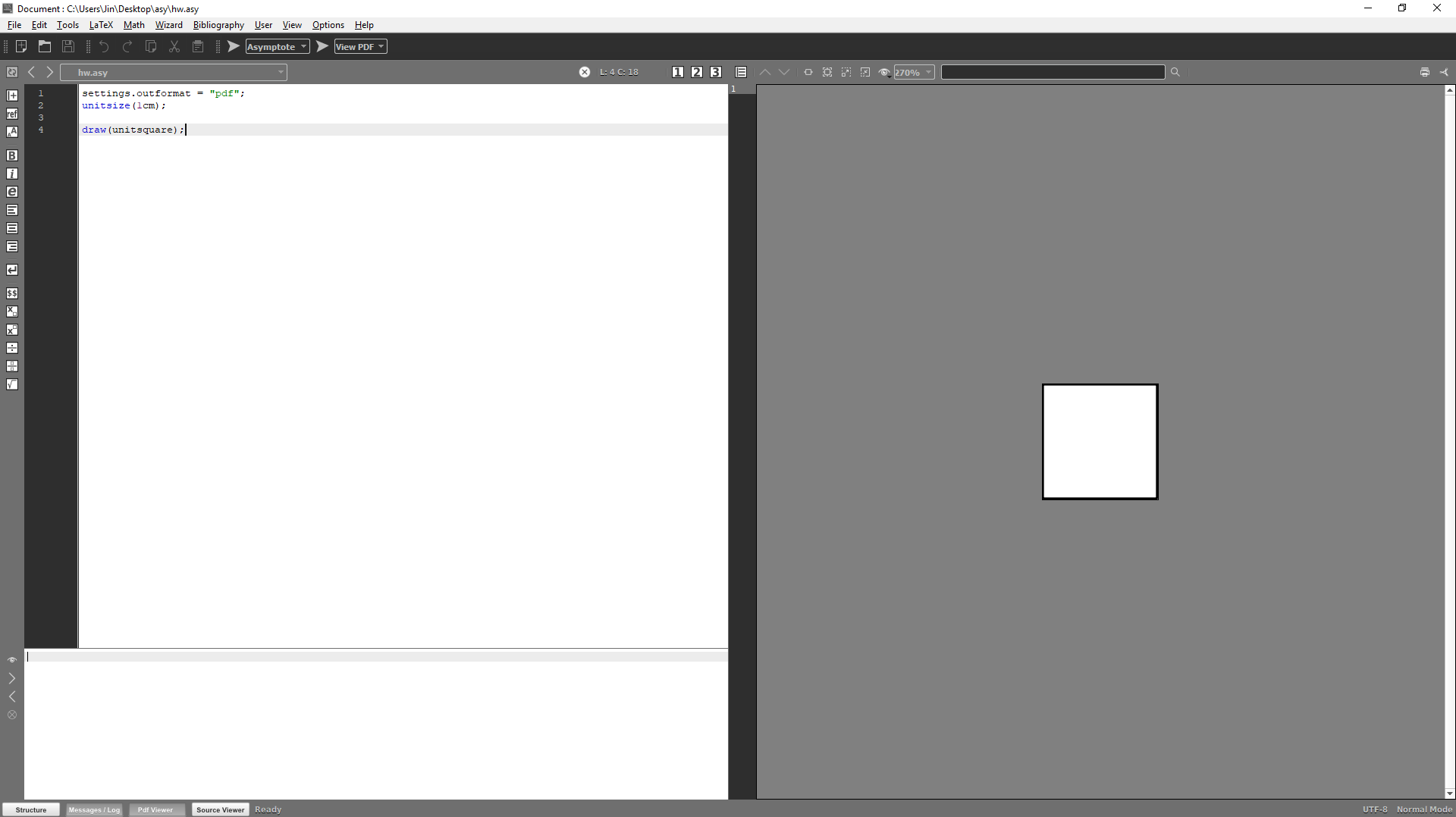
Pomocí příkazu draw(unitsquare); jsme nakreslili čtverec o hraně jednoho centimetru, a ten se vskutku na pravé straně zobrazuje. Pozadí našeho obrázku je ve výchozím nastavení bílé, nakreslily se tedy černé čtyři čáry na okraji. Obrázek byl následně uříznut na co nejmenší možnou velikost.

Popis syntaxe

Jazyk asymptote je podobný C nebo C++, např. komentáře se píší identicky pomocí //. Znáte-li jejich syntax, stačí si zběžně prolétnout následující sekci.

Proměnné

Jako v každém jazyce můžeme nastavovat proměnné, které mají různé datové typy, podle toho, co representují (a kolik místa zaberou). Zde je krátký přehled:

• Celočíselná proměná (integer), která se značí int
• Desetinné reálné číslo real
• Souřadnice bodu (dvojice reálných čísel) pair
• Křivka path
• Textový řetězec string
• Pole (array), neboli soubor proměnných. Píše se pomocí []

Proměnné je dobré nejprve deklarovat tak, že napíšeme typ proměnné a její jméno. Např. pokud napíšeme

	int pocitadlo;
	

tak jsme zavedli celočíselnou proměnnou jménem pocitadlo. Na konci každého příkazu se musí psát středník, jinak Texmaker vyhodí následují chybovou hlášku.

Proměnným lze dávat hodnotu např. takto:

	int i,j;
i = 2;
j = i^2 + 2*4;
i = i + 1;
	

Na konci těchto řádků bude i rovno 3 a j rovno 12. Zadefinovali jsme taky více proměnných stejného typu najednou. Dále lze také pracovat s textovými řetězci:

	
string a;
int i;
i=1;
a = (string) i;
a = a + "23ctyri";
	

Na konci tohoto příkladu bude a obsahovat textový řetězec 123ctyri.

Stojí za to poznamenat, že některé proměnné jsou tzv. systémové a mění nějaké parametry programu. Např. proměnná settings.outformat, kterou jsme potkali dříve, mění to, jaký výstupní formát budeme mít.

Funkce

Funkce jsou malé programy uvnitř programu, které můžeme definovat a posléze zavolat, aby pro nás vykonaly nějakou práci. Typicky ještě vratí výstupní hodnotu. Např. můžeme definovat funkci následovně:

	real f(real x) {
	return x*2;
	}
	

Tento kód říká, že funkce f bere jeden reálný parametr x a vrátí také reálný parametr. Můžeme ji zavolat následovně:

	real y;
y = f(2.1);
	

Potom proměnná y bude rovna 4,2. Ještě existují funkce, které nevrací parametr. Ty jen zavoláme, a ony něco vykonají (třeba nakreslí čáru).

For cyklus

Další důležitou věcí bude tzv. for cyklus. Pomocí něj můžeme vykonat mnoho věcí najednou. Např:

	
int pocitadlo;
pocitadlo = 0;
for ( int i = 0; i <= 2 ; ++i){
	pocitadlo = pocitadlo + 1;
}
	

Tento cyklus vykoná vnitřní kód pro i rovno nule, jedné a dvěma, tedy nakonec pocitadlo bude rovno třem.

Kreslení čar

Čáry se kreslí pomocí funkce draw(path p). Nejdříve však potřebujeme vědět, jak vypadá křivka path a bod pair. Bod můžeme definovat tak, že jednoduše udáme jeho souřadnice (nejdřív $x$ souřadnici, následně $y$). Předem se však hodí říci, v jakých jednotkách pracujeme (např. v centimetrech). Celkem můžeme mít např. takový kód:

	unitsize(1cm);
pair z;
z = (1,0);
dot(z);
dot( (0,0) )
	

Tím nakreslíme dvě tečky na dvou různých souřadnicích. Křivku můžeme definovat jako cestu přes nějaké body, následně ji můžeme nakreslit pomocí příkazu draw. Dále také záleží na tom, jestli chceme body propojit přímo nebo krouceně (pomocí tzv. Bézier křivky). Přímé propojení se dělá pomocí -- a kroucené propojení pomocí .., jak můžete vidět na následujícím příkladu;

	
unitsize(1cm);
path p1;
pair a;
a=(0,0);
p1 = a -- (1,1) -- (4,2) -- cycle;
draw(p1);
draw(a .. (1,-1) .. (4,-2) -- cycle);

	

Vyzkoušejte si, jaký obrázek dostanete. Horní je rovný, zatímco dolní je hladce propojený. Příkazem cycle se vrátíme cyklicky zpět na začátek.

Kdybyste v předchozím napsali ještě navíc fill(p1);, tak by se první křivka vyplnila černou barvou. Barvu výplně lze měnit (viz manuál s. 16).

Označení

Do obrázku lze ještě vložit text pomocí příkazu label( string nazev,pair posice). Samozřejmě nazev interpretuje LaTeX. Takže stačí napsat např. Stačí tedy zavolat třeba label( "$x^2$",(0,0)); a vysází se vám pěkné $x^2$ v počátku.

Příklad

Příklad všech ukázaných věcí je např. tento kód, který vyprodukuje očíslovanou osu, můžete si ji libovolně prodloužit:

	
settings.outformat = "pdf";
unitsize(1cm);

path osa;
real delka,prodl;

delka = 10;
prodl = 0.5;
osa = (-delka-prodl,0)--(delka+prodl,0);
draw(osa,Arrows );

path cara;
real rozpeti;

rozpeti = 0.2;

// Čáry do osy
for (int i = 0; i <= 2*delka ; ++i) {
	cara = (-delka+i,rozpeti) -- (-delka+i,-rozpeti);
	draw(cara);
	label((string) (i-delka),(-delka+i,-rozpeti*2 ));
}

for (int i = 0; i <= 2*delka*10 ; ++i) {
	if ( i % 10 != 0) {
	cara = (-delka+i/10,rozpeti/3) -- (-delka+i/10,-rozpeti/3);
	draw(cara);
	}
}
	
	

Kreslení grafů

Do asymptote můžete načíst i takzvané moduly (neboli knihovny, balíčky), což jsou rozšíření funkcí programu, které napsal někdo jiný. Jeden takový balíček se nazývá graph a dovoluje nám kreslit grafy funkcí.

	
settings.outformat="pdf";
unitsize(1cm);

import graph;

real f(real x) {
	return sqrt(x) + cos(pi/x) + log(x);
}
path g = graph(f,0.01,2);
draw(g);

	

Zde jsme křivku g určili pomocí funkce graph. Více o funkcích a o tom, jak je udělat jemnější, naleznete ve zmíněném tutorialu na str. 28.

Shrnutí

V programu Asymptote lze kreslit pokročilé obrázky způsobem, který jsem výše načrtl. Doufám, že nyní máte rámcové porozumění toho, jak takové obrázky kreslit. Vysvětlovat více funkcí jako např. kreslení geometrických tvarů či transformace by již tento text udělalo příliš dlouhý a hlavně by to bylo zbytečné: potřebné informace lze nalézt jednoduše na internetu nebo v odkazovaném tutoriálu a manuálu.

Jestli vám návod připadal užitečný, koukněte se i na ostatní Návody či na některé mé články. Doporučit mohu např. Oživlou geometrii, jednoduchý úvod do diferenciálního počtu.