I have broken down my article on calculus into several chapters. Each discusses one closed problem more or less from real life, but always an unusual one. To address this problem, we need to build new mathematical tools, which form the main thrust of the chapter. The whole series then tends towards a poetic fundamental theorem of differential calculus, which shines a new light on previous articles and opens up a lot of new perspectives on problems from physics. I don't anticipate much mathematical knowledge throughout the series, so perhaps anyone can understand the explanation. Mathematical ignorance may also be an advantage, for one can accept new ideas without worrying about previous misconcepts. Then, at the end of the series, as an addition beyond the anticipated knowledge, I attach derivations and integrals of some functions (I'll explain what this is about) together with a clear table.
English physicist Isaac Newton came up with the so-called Law of Force (2nd) in the 17th century. Newton's Law) to explain the movement of the bodies. According to him, the bodies move because of forces that give the bodies acceleration. So it means that if we impress a force of $F$ on a $m$ body, then the body gets an acceleration of $a=F/m$. Accelerating, for example. $100\,\mathrm{m/s}^2$ while doing so means that in one second the body will increase its speed by $100\,\mathrm{m/s}$. In school, everyone can then learn that if a body has some acceleration, then you can simply calculate what trajectory it travels in time.
The examples mentioned are reminiscent of aphorism The more Emmental, the more holes, the more holes, the less Emmental, ergo the more Emmental, the less Emmental.\u201d With Emmental we can discern a logical error, but the examples mentioned do indeed require something more.
This would mostly close the story on Newton, but let's be a little nosy. What happens when the force acting on a body changes somehow? For example, when a parachutist falls with a parachute, that's when the parachute is pushed by air, which slows it down. But, of course, the slower it falls, the slower the air hits the parachute, and thus the braking power diminishes. The faster it falls, the more it slows down, but the slower it falls, and the less it slows down... What, does that make sense? Or imagine a Saturn V rocket coming out of the atmosphere. This rocket, which carried men to the moon in 1968, burned 20 tons of fuel per second and made up 85 percent of its mass. Everyone knows that the lighter something is, the better it accelerates, so Saturn V was accelerating more and more with every second, but how exactly?
The calculus can explain, for example, the aforementioned events and much more. It is also sometimes called the infinitesimal number, since it uses infinitesimal (i.e., infinitesimal) quantities to explore the process, working with infinities. Typical of the differential count is the following question: What came first, average speed or instantaneous speed? I.e., is it easier (mathematically) to say that I was doing an average of 100 from Prague to Brno, or that I was doing 40 on my bicycle?\u201d Most people would say that instant speed is easier, but it is the fault of the walkway. Traditionally, we introduce average speed first as the total distance traveled over the total time, and instantaneous speed is just average speed measured over infinitesimal time.
Introducing yourself to differential calculus requires a little patience, and an open mind, and some of the things we encounter along the way seem counterintuitive, and you may be reluctant to accept them. As a demonstration of the trickiness of treating the infinite, we'll look at different types of numbers in the rest of the chapter, then in the next chapter we'll throw in something that's already more relevant to the subject. Let's stick to our motto path: if it were straightforward, it wouldn't be so interesting!
We often count things on our fingers: 1, 2, 3,... The numbers we use for this are called natural (they don't contain zero). With these natural numbers, we can simply describe how much something is. For example, we have a sack of potatoes and we can say there are 21 potatoes in it. Or that yesterday's raindrops are 210,929,293, or would go to express the number of grains of sand on the beach. But what if we put all the natural numbers in a bag (e.g. write them on paper), how many would there be?
A lot of mathematical knowledge is easy to come by if we look at the problem studied from a different point of view. Often, the introduction of markings will help to increase clarity. That's why we usually name mathematical concepts with single-letter names. They can then be combined with each other effortlessly, creating more complex concepts that we can once again name. At the same time, we sometimes name things we don't yet know. A name, as it happens, helps you know the thing.
Let's say we put the numbers in the bag in order. Then if we wanted to say that there's 1,000 of them, the highest number would be 1,000, we forgot 1,001! We'd add it, but then again, 1,002 are left out. And so on and on. Thus, the number of natural numbers in the bag cannot be described by any number. What you want to say is that there's infinity, but because you're reading a text about a differential number, we're going to describe that infinity in more detail. Mathematicians would say that a bag of natural numbers is a set, and that the number of numbers in it is its magnitude. For example, the set of numbers $\{ 1;\, 2;\, 3\}$ is a set of numbers containing the numbers 1, 2 and 3, and its cardinality is 3 because it contains 3 elements. We call the set of natural numbers $\mathbb{N}$ (the altered letter N), and its cardinality is no number, instead calling it $\aleph_0$ (alef zero; alef is the first letter of the Hebrew alphabet).
We've named the probability of natural numbers, but we haven't learned anything about it. Let's compare it to the magnitude of other sets. Consider the set of even natural numbers that includes 2, 4, 6, 8, 10... While the two sets are infinite, they can be compared to each other. Let us act like shepherds who want to count two flocks of sheep. Sheep are numerous and difficult to read. But we can always match a sheep from one flock to a sheep from the other flock and send them both away. If we can pair all the sheep like this, they're the same in both herds. But if, for example, in the first herd all the sheep are assigned to the second herd and there are still some left in the second, then the second herd is larger.
This is amazing, because this way could be applied to infinite sets. So let's try to compare the two sets in question as shepherds. We have a set of $\mathbb{N}$, in which there are numbers. We're going to name some number in that set $n$. Let's call the second set of even numbers $2\mathbb{N}$ and some number from that set $m$. First, let's match sheep from $\mathbb{N}$ to sheep from $2\mathbb{N}$. For every $n$ number we can think of, we select $m=2n$ from an even set. So we assigned to each number from $\mathbb{N}$ a unique number from $2\mathbb{N}$ as in the figure below.
Natural numbers are named after the letter N from the word natural (Latin for natura means nature).

Now let's try the reverse assignment: from $2\mathbb{N}$ to $\mathbb{N}$. Let's give each $m$ number $n=m/2$. The $m$ number is even, so $m/2$ does indeed belong to $\mathbb{N}$. In this way, each number from $2\mathbb{N}$ gets a unique number from $\mathbb{N}$. We can visualize the assignment as the diagram above with only the inverted arrows.
So we were able to pair the two study sets one-to-one. But that means they have the same bulk! This may come as a surprise, as a set of even numbers is created by taking odd numbers, infinitely elements, from a set of natural numbers. Still, the set size doesn't change, it just shows that it's meaningless to ask how much infinity minus infinity gives.
Perhaps the same size of the two sets studied can be better understood if we look closely at their elements. What if we didn't write $\{2;\,4;\, 6;\dots \}$ in a set of even numbers, but $\{2\cdot 1;\, 2\cdot 2;\, 2\cdot 3;\, \dots \}$? In counting elements, it doesn't matter if we count one, two, three, four, or if we count two times one, two times two, two times three, two times four. So it makes sense that the elements in both sets are the same.
Multiplies with a massive $\aleph_0$ are called countable sets. Intuitively, it means that if we had an infinite amount of time to use, we could list all of their elements. But there are also sets with even more heft than $\aleph_0$, which are called uncounted.
You guessed correctly what the real numbers of $\mathbb{R}$ are based on. But the real name has nothing to do with real-life use, distinguishing it from the so-called imaginary numbers invented in the 17th century by Ren\u00e9 Descartes, the same Descartes who invented, for example, the Cartesian coordinate system, in the writings of meditation on first philosophy, wondering if we happened to be living in a simulation (like Neo in the Matrix) and, above all, famously saying I mean, I am. ([Ego] cogito, ergo sum.).
One of the innumerable sets is a set of real numbers, $\mathbb{R}$. We need to measure something from time to time, and for that purpose, the real numbers shine. We take a meter to measure, and on it we read numbers like 2.3 (centimeters) and 6.91 (centimeters) or 0.242 (millimeters). Numbers of this kind are real numbers. We include zero in the real numbers as well as negative numbers, they include all natural numbers. At the same time, we think that meters can reach any length we want (or we can choose other units per meter), and that we can have a meter as accurate as we want. By precision, we mean that we can measure millimeters, tenths of millimeters, and millionths of millimeters, etc., on the meter, that is to say that real numbers can have any number of decimals, and they can be any size.
Compare now the set of $\mathbb{N}$ and $\mathbb{R}$. Let's try to do it like we see in the picture.

Here it can be seen that the natural numbers are noticeably less than the real ones, and it shows why the real numbers are called the innumerable set. Because if we were counting real numbers from one, even with infinite time, we wouldn't get to 1.2! So the mohotness of real numbers is greater than the magnitude of natural ones.
The claim about the magnitude of real numbers could be proved more mathematically, but I prefer to show another thing instead. And that is that the set of real numbers in the $0 to $10 range has the same size (cardinality) as the set of real numbers in the $0 to $1 range. The process will not change much from the last consideration. We will name the first set $\mathbb{R}_{0,1}$ and the second set $\mathbb{R}_{0,10}$. Try assigning elements first to second: any number $r$ of the $\mathbb{R}_{0,1}$ gets the assigned number $s=10\cdot r$ of $\mathbb{R}_{0,10}$.

The question is whether there are sets of numbers with a faculty between $\aleph_0$ and $\aleph_1$. This question is called the continuum hypothesis in mathematics. Related to the question is the work of Brno mathematician Kurt Gödel and his famous line about incompleteness. Unfortunately, however, we will not dwell on this, as it falls more within mathematical logic.
Conversely, we can assign to any element $s$ of the $\mathbb{R}_{0,10}$ another unique element $r=s/10$, which belongs to the $\mathbb{R}_{0,1}$ (equivalent to reversing the arrows in the picture above). What we've achieved is we've created a one-to-one, unambiguous pairing of elements from both sets. For each element from $\mathbb{R}_{0,1}$, we have exactly one element from the set $\mathbb{R}_{0,10}$, and so the sets have the same faculty. Once again, the sets can be broken down as $\{0,12;\, 0,38;\, 0,2189;\, 0,11;\dots \}$ and $\{10\cdot 0,12;\, 10\cdot 0,38;\, 10\cdot 0,2189;\, 10\cdot 0,11;\dots \}$, so perhaps their comparison will no longer be surprising.
Using a similar trick as above, it can be shown that any interval of $\mathbb{R}$ has the same magnitude as any other interval, even as $\mathbb{R}$ itself. This magnitude is called $\aleph_1$. Perhaps this strikes you as odd, but such a property of real numbers comes in handy when describing our world. Consider, for example, time. This is measured using real numbers (e.g. in seconds), however, there is no smallest time unit (not a hundredth of a second, not a thousandth). The requirement that any small moment can be divided as subtly as possible gives us hope, because it means that time flows continuously, without twitching.
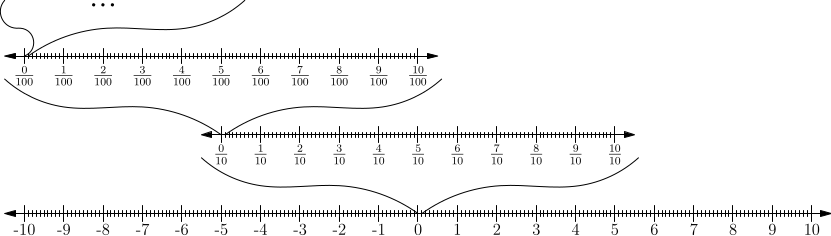
This unusual insight into the dense nature of real numbers seems to me to be a fitting starting point for the essence of differential calculus. Those statements about infinity may have surprised you, and you may not want to believe them. Be that as it may, these are mathematically consistent insights, the harder task of knowing how they relate to our real world. Perhaps, then, the following articles will offer an appropriate perspective.