So we became familiar with a differential equation that models an oscillating quantity and looks like this. $$ f''(x) = - \omega^2 f(x)$$
has a solution $$ f(x) = A \sin(\omega \, x + \varphi ) \,,$$
where $\omega$ and $\varphi$ are some constants. We named the plot described by this equation the harmonic oscillations. Like with an exponential equation, we can use a harmonic oscillator to define the function sine (and cosine). Here, we'll show where we can meet such a harmonic oscillator. These will now mainly be purely physical, mechanical examples. It's a bit of a shame we don't welcome other industries, but we imagine a principle by which a harmonic oscillator can be found in almost any physical system.
A simple spring with a weight forms such a prototype harmonic oscillator, so we'll look at it first. Her drawing can be seen in the picture below.
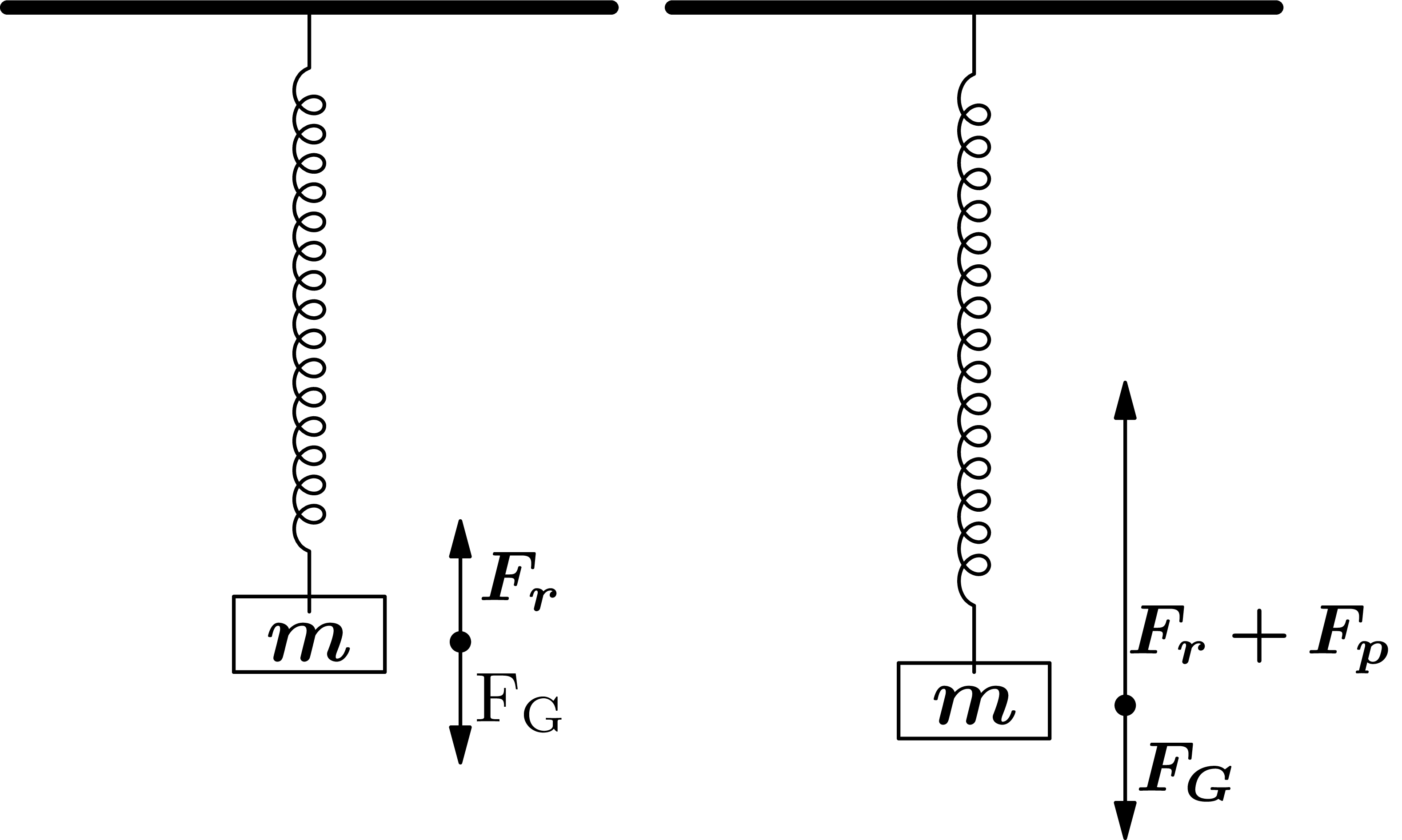
We've plotted the force's location outside of the $m$ weights for clarity. In the left-hand part of the sketch, we have a case where the spring and the weight are in equilibrium -- the reactive force of the spring $F_r$ exactly equals the gravitational force of $F_G$. But if we tilt the weights a little, as is the picture on the right, then the force of the $F_r$ spring increases by the addition of $F_p$, and we are already in an imbalance. Our job will be to figure out how the spring will keep moving.
To detect the next movement, we need to determine what force the spring exerts. Empirical measurements show that typical springs react linearly to the displacement: that is, the reactive force of the spring is proportional to the displacement over a constant called spring stiffness $k$. Mathematically, we write it down as follows: $$F_r = - k\cdot x\,,$$
where $x$ is an offset from the equilibrium position. Given the linearity of the force, we can imagine that the first spring position is already the starting position. This means that the $F_r$ and $F_G$ forces will not be considered as they cancel out, and the dynamics will only be due to the addition of the $F_p$ force. So we can write Newton's Law of Force to figure out the movement equations of the weights: $$\begin{align*} F = m \cdot a \Rightarrow F_p &= m \ddot x \\ m \ddot x &= - k x \\ \ddot x &= - \frac{k}{m} x\,. \end{align*}$$
We can solve this equation because it's an equation of a harmonic oscillator from the beginning of a chapter. We get: $$\begin{align*} x(t) &= x_0 \sin\left( \sqrt{\frac{k}{m}} \, t + \varphi_0 \right)\,. \end{align*}$$
Here, integration constants have meaning for the initial displacement in the case of $x_0$ and $t_0$ so-called initial phase. We see that, for example, at $\varphi_0 =0$ and $t=0$ is $x(t)=0$. This means that with this $\varphi_0$ option, we start to see when the body is in zero displacement. In general, the phase tells us when we start to observe the plot, you notice that we can reset any phase if we just let time go long enough -- the sine is periodic. Next, note that the quantity $\sqrt{k/m}$ determines how fast we oscillate. So this is, in a sense, the angular frequency of $\omega$. Apparently, more spring stiffness means faster oscillation (there's more reaction force), just as less mass $m$ means faster oscillation.
Let's stick with mechanical systems for a moment and look at another oft-dropped example of harmonic oscillations: the mathematical pendulum. We have prepared the sketch again below.
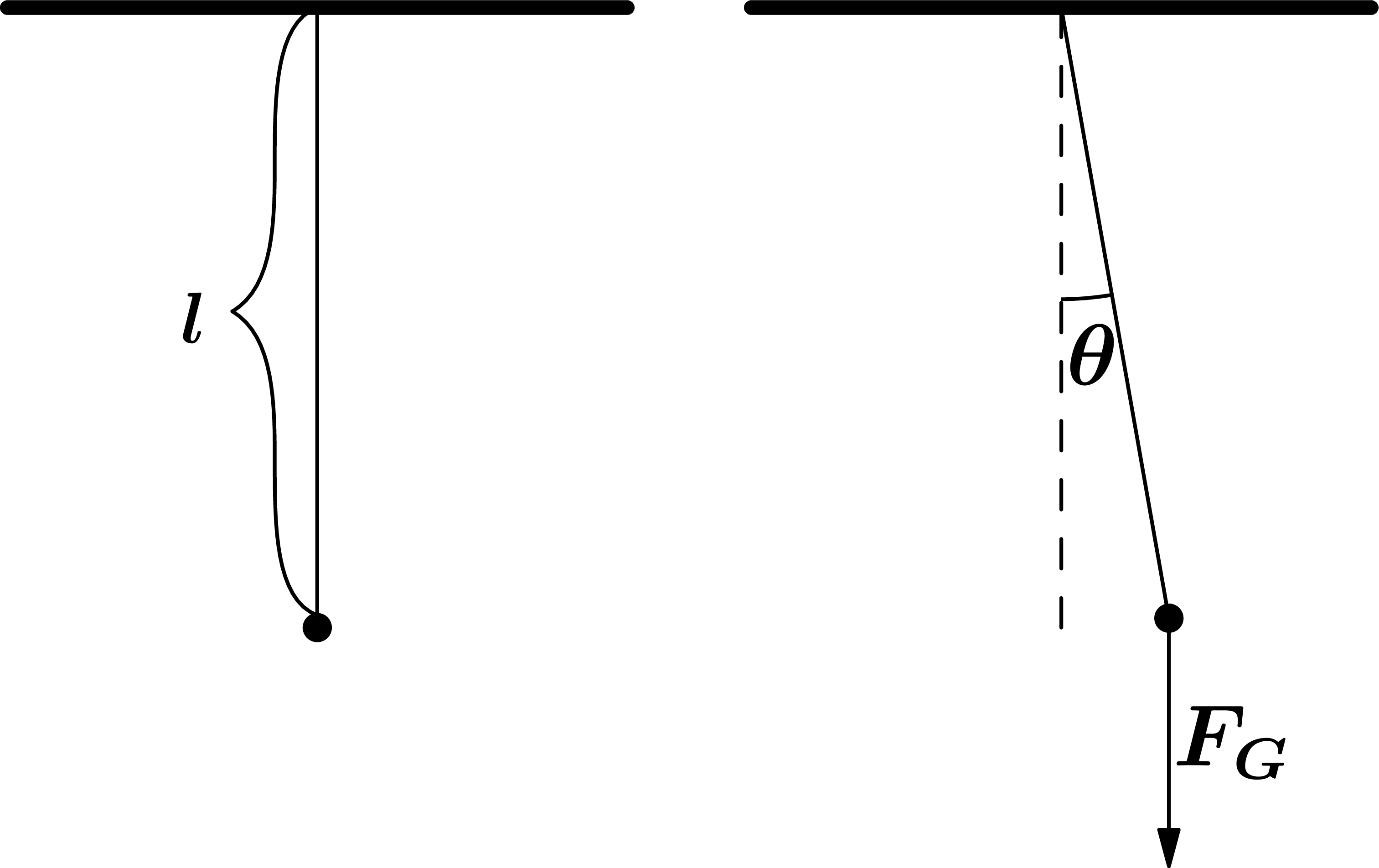
In the first case, the pendulum hangs motionless, the gravitational force is offset by the pulling force from the rope-nor have we drawn such a simple decomposition of forces. In the latter case, the pendulum was slightly tilted by the angle $\theta$ (a small Greek theta). But the weight force exerted on the pendulum goes straight to the ground. We need to decompose the forces again so we can understand the pendulum's movement.
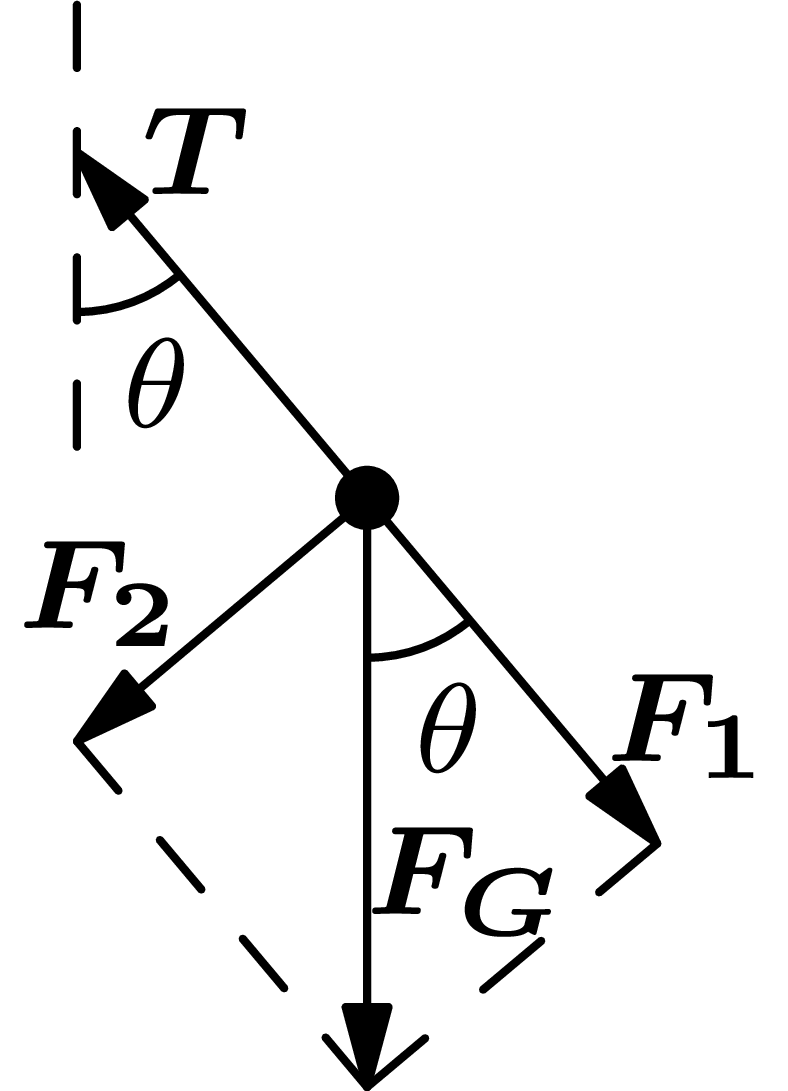
In this decomposition, we have spread the gravitational force of $F_G$ into two perpendicular components of $F_1$ and $F_2$. We see that the strength of $F_1$ is offset by the rope, while the other component of $F_2$ is not-causes the pendulum to move. At the same time, we can infer from the geometry of the situation that $$\begin{align*} F_2 &= F_G \sin(\theta ) \,. \end{align*}$$
Now let's do an approximation of the mathematical pendulum. For small angular displacements, we argue that we can write $\sin (\theta )\approx \theta$. This approximation is proven to be quite accurate in the pendulum example, plus in past chapters we have sometimes mistaken $\sin(x)$ for $x$. If we didn't do this approximation as is appropriate, for example, in the case of large displacements, we would get a physical pendulum, which is a significantly more complex model.
So we can write Newton's Law of Power: $$\begin{align*} F_G \theta &= m\cdot a \\ m g \theta &= m\cdot a \\ g \theta &= \ddot x \,. \end{align*}$$
What remains to be explained is the significance of $x$-it's the distance that the pendulum travels on its trajectory there (positive $x$) or back (negative $x$). In the case of small displacements, the trajectory is almost the same as the parallel $x$ axis. In the equation, we immediately see the term $\ddot x$, which promises us a differential equation. But we can't integrate right away, because the angle of $\theta$ also depends on $x$ so we have to express it as $$ x = l\sin(\theta) \approx l\theta\,.$$
We put this in our equation and we get: $$\begin{align*} \frac{g}{l} \, x &= \ddot x \,. \end{align*}$$
In this, you can recognize the harmonic oscillator equation at the beginning of the chapter, so we can write a solution: $$\begin{align*} x(t) &= x_0 \sin\left( \sqrt{\frac{g}{l}} \, t + \theta_0\right) \,. \end{align*}$$
For the first integration constant, we chose $x_0$ as the highest possible deviation: indeed, the sine has the highest value of one, so $x_0$ is the highest possible deviation. Next, $\theta_0$ indicates the stage we talked about earlier in the spring.
Let's go back to the realm of electrical circuitry. In chapter 6, we always had either a coil or a capacitor in one circuit, and the result was a first-order differential equation. This time we'll try to put a coil and a capacitor in one circuit, and we'll get a so-called LC circuit. His picture is below.

Let's get the voltage on both components back from equal. Then we adjust everything to get the differential equation in one variable: charge. $$\begin{align*} -L\dot I &= Q/C \\ \ddot Q &= -Q/LC \,. \end{align*}$$
This is already a standard form of our harmonic equation that we can solve: $$\begin{align*} Q(t)&= Q_0 \sin\left(\sqrt{\frac{1}{LC}} \, t + \varphi_0 \right) \,. \end{align*}$$
The $Q_0$ integration constant indicates the initial charge in the circuit. The second integration constant of $\varphi_0$ is traditionally a phase that we have already interpreted. Note that the angular frequency of the circuit is $\omega = 1/\sqrt{LC}$. This is a known resonance frequency that occurs frequently in capacitor and coil circuits.
One physical quantity was suspiciously absent from the brief presentation of body movement and Newton's laws: energy. Each concept of energy sort of knows and maybe has used it to describe examples, but can it be used to describe the movement of bodies? Most of the energy is used to describe the initial and final state, e.g. the potential energy of a boulder on a hill and the kinetic energy of a boulder after a downhill run. Can this description be extended to instantaneous movement?
Yes, we encountered a similar problem here as the distribution between instantaneous velocity and average velocity: instantaneous velocity is just the average velocity in a very small time. So a derivative will help us to connect energy to kinematics.
So let's take a body with a potential energy of $V(x)$. The energy here is denoted by the symbol $V$ (not $E$) according to Joseph-Louse Lagrange, who chose this letter according to the French word voltage. In contrast, the kinetic energy would be $T$ according to the French travail (work). We're also writing $V(x)$, which means that the energy of a body is only dependent on its position $x$ (generalizing into $3D$ space can be done, but it's too lengthy). As an example of a body with a potential energy of $V(x)$, you can imagine a rock in the Earth's gravitational field with energy of $V(x)=m g x$, where $m$ is the mass of the body and $g$ is the gravitational acceleration.
The trick is to realize that potential energy is expressed by work that is equal to the force of $F$ times distance. So let's imagine a body in some default position of $x$, where the force of $F$ is acting on it. If we move the body a small distance $\mathrm{d} x$, it changes its potential energy by increments $$\mathrm{d} V(x) = - F \mathrm{d} x \,.$$
The minus is here because when the body moves in the direction of the force (e.g., falls a little), the energy decreases. On the contrary, it has to move in opposite directions to increase its energy. Then surely we won't be surprised that a relationship pays $$F(x) = \frac{\mathrm{d} V(x)}{\mathrm d x} \,.$$
How can we interpret this equation? Simply: the bodies move to a state with as little potential energy as possible. Let it have the potential at some point of the $x$ positive derivative. That means if we raise $x$, the potential increases. But our equation tells us that the force will work in the opposite direction: the body will always try to minimalize its potential energy. In the case of stone, it becomes a fall.
So if we know the distribution of potential, we can calculate the force using its derivative. In the example with the stone, we simply get $F(x)=-mg$ (acts down), which is a familiar term for gravitational force. Of course, if the Earth's gravitational field were to be considered non-homogeneous, or e.g., the moon's gravitational pull, then the force would really depend on $x$ and be more complex.
How does this relate to the harmonic oscillator? The key lies in potential. Let's imagine that at some point $x=x_0$ has the potential to have a local maximum. How would we calculate the value at point $V(x_0 + \Delta x)$? In Reviving Geometry, we have similarly calculated the square roots: just take the derivative: $$V(x_0 + \Delta x) \doteq V(x_0) + \Delta x V'(x_0) \,.$$
But wait, the derivative is zero, because we're at maximum! So the potential doesn't seem to be changing. But that's not really true, we need a better estimate. It turns out that the Taylor method of development can give us a good guess: $$V(x_0 + \Delta x) \doteq V(x_0) + \frac{1}{2} (\Delta x)^2 V''(x_0) \,.$$
Notice here that $V(x_0)$, the second derivative of the $V(x)$ function at point $x_0$, is just some number. So we express the potential as some kind of parabola -- it turns out to be a tangent parabola. We used a tangent line before, we have a parabola for precision. In general, Taylor's development will offer a tangential polynomial. A graphical representation can be seen in the following figure \u2014 in the near vicinity of point $x_0$, we consider $V(x)$ as the parabola shown.
We used a chain rule here for derivatives. Now we have to answer the question of what is the change in $\Delta x$ s by $x_0 + \Delta x$. To do this, you just need to cleverly add and subtract $x_0$: \begin{align*} \frac{\mathrm d \Delta x}{\mathrm d (x_0+\Delta x)} &= \frac{\mathrm d (x_0 + \Delta x) }{\mathrm d (x_0+\Delta x)} + \align{\mathrm d (-x_0) }\mathrm d (x_0+\Delta x)}= 1 + 0 = 1 \\\\\.\
You can understand the result by saying that a change by $x_0 + \Delta x$ is the same as a change by $\Delta x$, because $x_0$ is a constant and does not change. So we can continue to calculate the derivative of potential: $$V'(x_0+\Delta x) =\frac{\mathrm d}{\mathrm d \Delta x} \left(\frac{1}{2} (\Delta x)^2 V''(x_0) \right) = V''(x_0) \frac{1}{2} 2 \Delta x = \Delta x V''(x_0)\,.$$
If we can express force, let's just make Newton's Law $F = m \Delta \ddot x$! This one looks like this $$m \Delta \ddot x = -\Delta x V''(x_0) \Rightarrow \Delta \ddot x = - \frac{V''(x_0)}{m}\cdot\Delta x \,.$$
I'm sure you recognize in this the harmonic oscillator equation from the beginning of the chapter. Just here this time we're looking for the $\Delta x(t)$ function, or the $\Delta x$ offset from the original $x_0$ position, as they evolve in time. The best thing about the whole thing is that potential energy is a general concept that can be created for almost any situation. It gave us a way to express every mechanical problem around balance like a harmonic oscillator.
It involves swaying a bridge, bending a table, closing a door, rocking a boat on water, and many other analogous problems. But understanding this principle will open up a new understanding of existing non-mechanical problems, such as the electrical circuit. Moreover, more complex designs can be built on the concept of a harmonic oscillator. For example, a simple model of a substance made up of atoms considers that atoms behave like harmonic oscillators, which is still very accurate. Intermolecular forces are often thought of as harmonious. In quantum mechanics, we find a deep expansion of the harmonic oscillator. It is, in short, a device that any physicist will use whenever he can.