In the last chapter, we watched a falling stone to sample a differential equation. We describe the movement of the stone in a foreign word as translational, to highlight that it is moving on some trajectory. In contrast, the subject of this chapter will be rotational motion and the related question of coordinate systems.
We mentioned that differential equations are used to introduce new functions. In this chapter, we'll talk about two new, so-called goniometric functions. We will present them independently of the differential equations, but we will clarify the context later.
The concepts we present in this chapter are not modern at all. All the examples could have been solved, or solved, by Newton himself when he started the differential. These are somewhat outdated problems in terms of the evolution of mathematics: while other areas of mathematical analysis are still in bloom, the problems presented here have long been solved by humans and are now taken for granted. But it is ironic that the same problems, solved on paper with sweat on their faces by 18th-century European mathematicians, are now being exploited in a very different field: the development of computer games.
Coordinate systems are absolutely crucial for a computer to know where a player, enemies and game objects are located. Moreover, things are moving, and so the movement equations need to be solved to make things realistic. Of course, computational methods have shifted somewhat over 300 years, and computers solve equations numerically, by brute force. Still, it's important for game developers to know concepts so they don't bring any glitches to the game.
To begin with, let's look at another question that Isaac Newton addressed -- the water bucket problem. So let's imagine a bucket of water on whose handle we tied a rope. We slowly turn this rope around our axis (about the same as when we squeeze a towel). Then we let go of the rope and the bucket and the water begin to spin.
We're all familiar with the spin motion-the carousel, the yo-yo, the blender, the wheels of the car, the Earth around the sun, all perform a spin motion. Anyone who has been on the merry-go-round knows firsthand what centrifugal force is present in rotational motion. The question remains, however, how to discern rotational motion from a physical point of view and exactly when we will meet centrifugal force. For the translational motion of the last chapter, we made do with the relative movement of the bodies relative to each other, but the example above shows that we can no longer use this: before spinning, the relative movement of water relative to the bucket is zero, and after spinning, too. Yet the two situations differ in that we detect centrifugal force in one and not in the other.
It may seem like a quibble, but it actually hides a deep thought. For all of us will probably accept that translational movement is relative: for example, we cannot tell if a train is moving towards the ground or the ground towards the train. But rotational motion carries forces: we accept that if we spin a carousel, we will feel centrifugal force on it. But if we spin the whole world and let the carousel stand, should we create some power on the carousel? We'll take a closer look at that now.
To describe the rotational motion of a rigid body, we have to describe the rotation of each individual point in it. This rotation just happens to be the movement of that point around the circle and that's a situation that we can imagine very well, see the picture.

We're getting a little deeper into the realm of physics, so we have to imagine a somewhat technical concept: a coordinate system. Everybody kind of assumes that we're moving in space, but as humans, we also want to navigate space. So we're introducing a coordinate system, which is a way to assign each point a unique set of numbers -- coordinates that uniquely describe its position in space. Each place will be marked with a different set of numbers, and we won't get lost in space.
It doesn't seem so, but the invention of Cartesian coordinates allowed the mathematicians of the time to connect geometry and algebra, which until then had operated separately. For more on this miraculous connection, see Steven Strogatz's Infinite Powers.
The most popular coordinate system was invented in the 17th century by Rene Descartes, and his number is called Cartesian. We're going to focus on a two-dimensional (2D) space, or a sheet of paper, for example. To describe the points on it, we first choose the origin and two perpendicular lines passing through this point. Each point gets two coordinates: $x$ and $y$ indicating its height and length along two axes. So the beginning has a position of $x=0$, $y=0$, which we write as $(x,y)=(0.0)$.
Cartesian coordinates can be used in many situations, but they don't really fit the description of rotation. That's why we're introducing polar coordinates that are directly adapted to rotation. Again, we have to choose a fixed point with the coordinates $(0.0)$ and one line that goes through it. The distance from the starting point of $r$ and the angle of $\varphi$ from the line (measured clockwise) will now serve as coordinates - see the picture.

Note that in both cases the position of the body is clearly determined by two parameters: either $x$ and $y$, or $r$ and $\varphi$. The only ambiguity is for $r=0$, it doesn't matter the $\varphi$-value - programmers have to be careful about that.
The word goniometric comes from the Greek gonium, which means horn. So you could say that these are functions of cornucopia.
Both Cartesian and polar coordinates describe all points in space. So we should be able to cross between them. So let's look at how we get the Cartesian from the polar coordinates. But we're going to have to imagine two new functions -- the sine and the cosine, which, along with other similar ones, we call the goniometric functions.
The introduction of sine and cosine functions is based on the need to effectively describe right triangles, which is used in e.g. surveying. So let's imagine a general right triangle of ABC with sides of $a$, $b$, $c$ and angles of $\alpha$, $\beta$, $\gamma$:

The sum of the angles in a triangle is always $180^\circ$, so obviously $\beta = 90^\circ - \alpha$. We also know that to draw a triangle, we need to know at least three of its data. This is a right triangle, so we already know one of its angles. So to draw a triangle, you just have to add the length of its side $a$ and the angle size $\alpha$.
However, it turns out that the length of a $a$ side is less relevant to the determination of a triangle from a certain perspective than the size of the $\alpha$ angle - that is, right triangles with the same $\alpha$ but different $a$ are similar. Similarity is a mathematical concept that simply says that two similar triangles are bloated with each other, i.e., that we get one from the other only by scaling (multiplying by a constant).
The claim of similarity makes sense, because it actually corresponds to the fact that we measure the triangle in other units. For example, we can have a triangle with lengths of $a=3\,\mathrm{cm}$, $b=4\,\mathrm{cm}$, $c=5\,\mathrm{cm}$, but in the US they would measure it with inches. They would get different values $a_p$, $b_p$, $c_p$ in inches, but it would be the same triangle. In doing so, $a_p = k\cdot a$, $b_p = k\cdot b$ and $c_p = k\cdot c$, where $k$ is some kind of conversion constant
Furthermore, for two similar triangles, the ratio of their corresponding sides is the same. For example, $a_p/c_b=a/c$, which can be demonstrated as follows: $$\frac{a_p}{c_p} = \frac{a \cdot k }{c \cdot k} = \frac{a}{c}\,.$$
Related to this is the introduction of goniometric functions \u2014 for a triangle with an angle of $\alpha$, we use the following preservation ratios: $$\begin{align*} \sin (\alpha ) &\equiv \frac{a}{c} & \cos(\alpha ) &\equiv \frac{b}{c} \,. \end{align*}$$
Functions defined in this way can be used to figure out all sides of any right triangle. For we can write: $$\begin{align*} c &= \frac{a}{\sin (\alpha)} & b &= c \, \cos (\alpha) \,. \end{align*}$$
Meanwhile, we can measure the value of the $\sin (\alpha)$ function using a familiar triangle similar to our own, for example.
However, the goniometric functions defined above have certain flaws, such as that the definition refers to a triangle in which $\alpha < 90^\circ$. So let's expand the definition with a unit circle, see Fig.

The image could be generalized to three dimensions by adding an additional angle of $\theta$, which represents the rotation around the $y$ axis. This is very important for game development, but we are not going to deal with it for the sake of simplicity.
The image shows a great sense of goniometric functions: it is used to move from polar coordinates to Cartesian coordinates according to the following formula: $$\begin{align*} x &= r \cos (\varphi) \\ y &= r \sin (\varphi) \,. \end{align*}$$
These formulas are therefore definitional for the $\cos$ and $\sin$ functions. At the same time, the essence of the previous interpretation of goniometric functions is captured by triangles. In the diagram above, we have a right triangle with sides of $r_0$, $r_0\sin (\varphi)$ and $r_0\cos(\varphi)$.
Because of our circle, we can also expand the goniometer functions for larger angles than just $90^\circ$. For example, we see that the cosine of angles between $90^\circ$ and $180^\circ$ is negative. Next, angles larger than the full angle of $360^\circ$ rotate around the circle, giving us a periodicity (functions repeat). For convenience, we'll display the features in the following chart:
It is noteworthy that we no longer work with grades, but with natural angular units, so called radians. This basically means that the whole circle has an angle of $2\pi$, and the smaller angles are fractions of that angle -- i.e. $90^\circ=\pi/2$ (a quarter of a circle).
The most famous relationship, often used, is called the goniometric one. Perhaps a more appropriate name for it would be the goniometric Pythagorean theorem, since we can go from it to derive an identity: $$\begin{align*} a^2 + b^2 = c^2 \Rightarrow \frac{a^2}{c^2} + \frac{b^2}{c^2} = 1 \Rightarrow \sin^2(\varphi) + \cos^2(\varphi) = 1 \,. \end{align*}$$
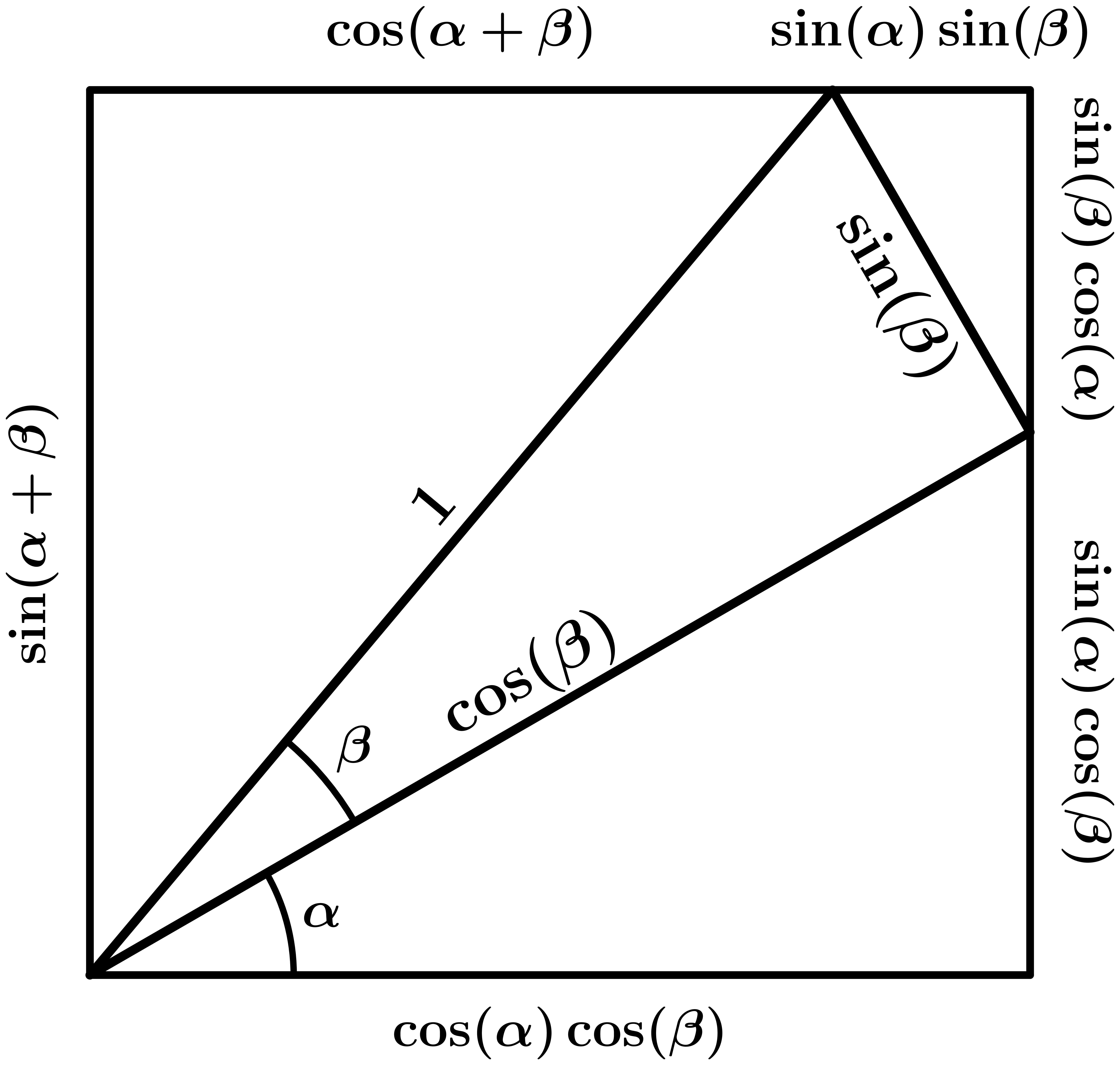
Note that just as the Pythagorean theorem applies to any triangle, the goniometric 1 applies to any angle of $\varphi$. We also know the sum formulas of the goniometer functions: $$\begin{align*} \sin (\alpha + \beta) &= \sin (\alpha) \cos (\beta) + \sin(\beta) \cos(\alpha) \\ \cos (\alpha + \beta) &= \cos (\alpha) \cos (\beta) - \sin(\alpha) \sin(\beta) \,. \end{align*}$$
The validity of the sum formulas can be seen from the following diagram:
These formulas can be used to derive a derivative of the goniometric functions, as we've already written in the derivative appendix of Living Geometry. To remind you: $$\begin{align*} \sin'(x) &= \cos(x) \,,\\ \cos'(x) &= -\sin(x) \,. \end{align*}$$
The more extensive goniometric insertion is behind us, now we can see how it is with the rotational movement. First, using polar coordinates. So let's imagine a point rotating around the center coordinate system at a distance of $R$ and try to find $r(t)$ and $\varphi (t)$.
Obviously, when rotating, the distance of the point from the center doesn't change, so we have $\dot r =0$ (note that the dot indicates the time derivative), so $r(t) = R$. The angle of $\varphi$ continues to change at a constant rate, which can be described as $\dot \varphi = \omega$, where $\omega$ is a so-called angular rate. By integration we get: $$\begin{align*} \dot \varphi = \omega \Rightarrow \int \dot \varphi \, \mathrm{d} t &= \int \omega \, \mathrm{d} t \\ \varphi (t) = \omega \cdot t + \varphi_0 \,, \end{align*}$$
where $\varphi_0$ is an integration constant indicating the starting angle (mostly equal to zero). In the Cartesian system we get: $$\begin{align*} x(t) &= r \cos (\omega t + \varphi_0) \,,\\ y(t) &= r \sin (\omega t + \varphi_0) \,. \end{align*}$$
All you had to do was take advantage of the system-to-system relationship. Now let's try to calculate the acceleration of a point that goes around the circle like this -- acceleration is the second derivative of the position by time, so we have to take the two co-ordinates $x$ and $y$ twice and we get it. More specifically, we get an acceleration in the direction of $x$ and an acceleration in the direction of $y$. So let's derive $x$: $$\begin{align*} \dot x(t) = \frac{\mathrm{d}}{\mathrm{d}t} r \cos (\omega t + \varphi_0) = \frac{\mathrm{d}r}{\mathrm{d}t} \cos (\omega t + \varphi_0) + r\frac{\mathrm{d}\cos (\omega t + \varphi_0) }{\mathrm{d}t} = 0 - r \sin (\omega t + \varphi_0) \cdot \omega \,. \end{align*}$$
In this calculation, we used first the product derivative rule, then the compound function derivative rule ($\omega t + \varphi_0$ is internal, $\cos$ outer) and most recently that the $r$ derivative is zero. Derivative a second time: $$\begin{align*} \dot x(t) = -\frac{\mathrm{d}}{\mathrm{d}t} r \omega \sin (\omega t + \varphi_0) = - r\omega^2 \cos (\omega t + \varphi_0) \,. \end{align*}$$
The coordinates of the $y$ would surely be similarly affected by the symmetry of the problem. The acceleration came out negative for us because we calculate that in the first few moments the $x$ position will only decrease as it starts at its maximum (case $\varphi_0=0$).
But we got an interesting result: the acceleration is non-zero and periodically changes as cosine in the case of $x$ (and sine in the case of $y$). Besides, the result tells us that the acceleration is happening at all. And that's a fundamental change from translational movement.
In a straight line (translational) motion in the direction of $x$, the $\dot x = v(t) = v_0$, but $\ddot x = a(t) = 0$. In contrast, in a uniform rotational motion, we have $\dot \varphi = \omega$, however, as we have shown, that movement is accelerated. So the necessarily standing observer is, from the point of view of the rotating observer, non-inertial.
Therein lies the key to understanding the paradox of the bucket. Rotational and translational movements are fundamentally different, and when we move from one system to a rotating one (e.g., from the ground to the carousel), we travel from the inertial to the non-inertial. This is what happens when forces occur.
So does this mean that if we spin the whole world and the carousel remains standing, we're going to bring strength to the carousel? Apparently so. Ernst Mach tried to elaborate on this interesting idea, and even then Albert Einstein answered it with his theory of relativity.
In the general theory of relativity, space and matter are inextricably linked by Einstein's equations-something the bucket paradox alludes to. Interestingly, though, while the concept of coordinate systems has helped us a lot in our analysis relativistically, we are trying to get rid of specific coordinates. For every observer's view of reality must be equivalent, which means that our description of reality should be independent of any artificial preconceptions. Coordinate systems (e.g., where they have a center is purely arbitrary and should not affect the theory) are also one such preconception, so a so-called tensor description is introduced that describes the world without the necessity a priori of choosing a specific coordinate system.
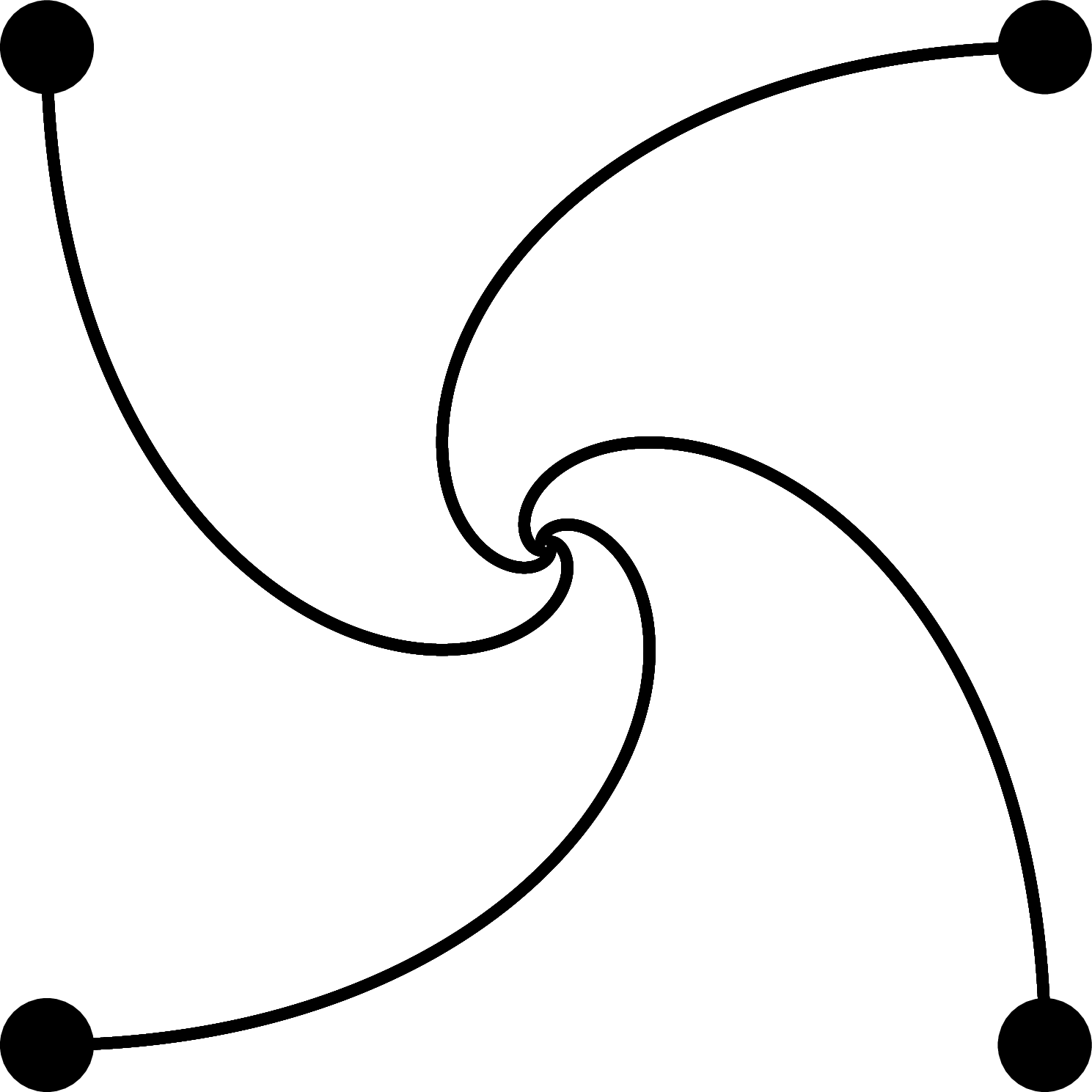
To complete the demonstration of the importance of coordinate systems, we will show one more daunting task. Let's imagine 4 dogs in the corners of a square room. Each of the dogs is aimed at the dog, which is clockwise to the right of it. Everyone runs straight for their goal, which means that at every moment their speed is on target. The situation is illustrated in the figure below.
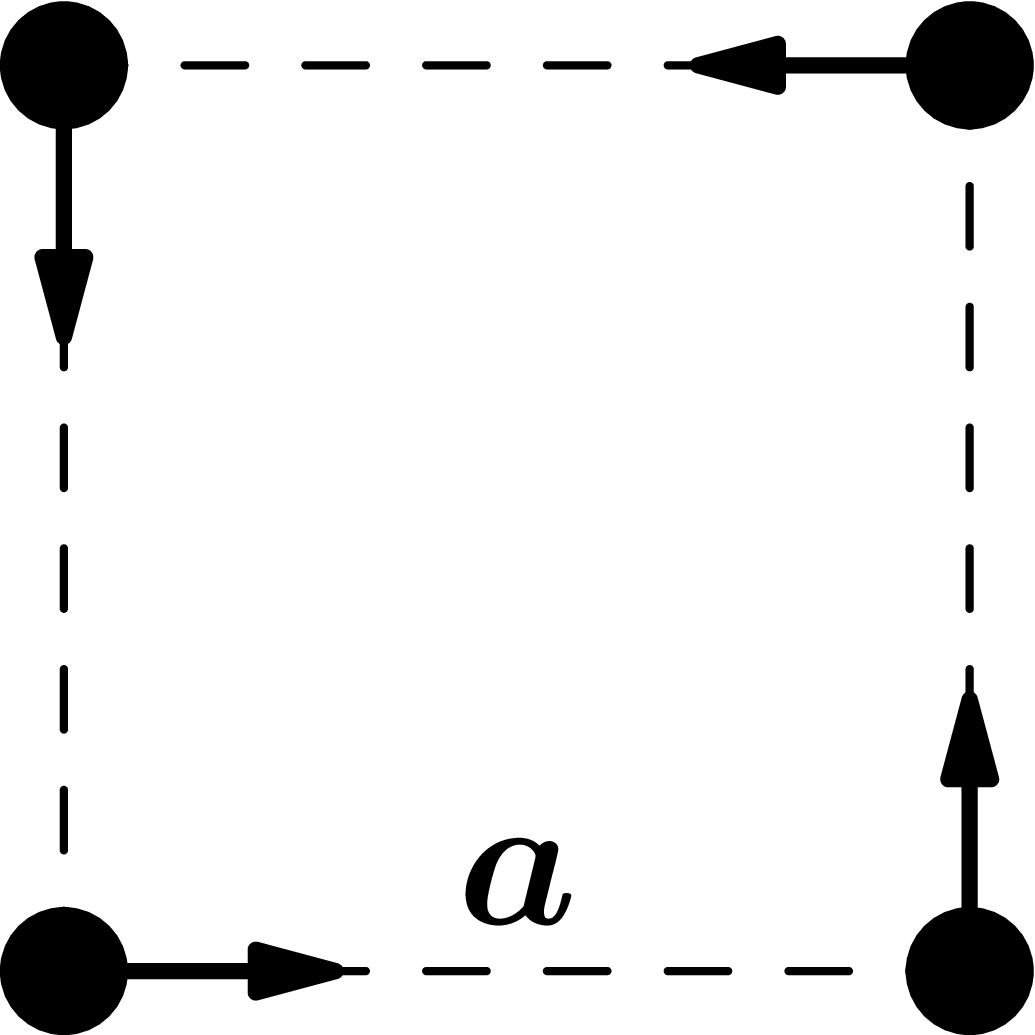
It's clear that the dogs won't be running on the square, because after a while, they'll all swing out of their original positions, so they'll change their direction of speed. It turns out that over time, dogs circle around to the center. If the speed of the dogs is $v$ and the original side of the square is $a$, how long before the dogs meet? And what will their running trajectory be? The answer to the second question already requires a differential number, but the first question can be handled without it (just use symmetry). Try to think if you can come up with the answer yourself.
First, let's answer the question of how long it takes for dogs to finish. According to the council, we're reminded of the rotational symmetry of the problem -- when we turn the shape from the input around the center of the room by an angle, we actually have the same configuration. Let's see what happens after a while while the dogs are running. Since both the initial spacing and the speeds of the dogs are symmetrical, the dogs will form a square again after each time.
What we also know is that the speed of dogs is going to be going along the circumference of the square at the beginning of the action. So it is after any amount of time, and from that we can conclude that at a rate of $v$, each dog will be reducing the prime distance of $a$. It will collide when it reaches zero, which is when $\tau = a/v$. To summarize our description, dogs move like a spinning, shrinking square whose edge is shrinking at $1 per cent.
Now to calculate the trajectory. We'll follow the dog in the lower right corner (the trajectory of the others will just be rotated) and choose the polar coordinates to describe it by starting with the dog $r(0)=a\sqrt{2}/2$ and $\varphi (0) = 0$. Let's look at the speed of the dog. We can break it down into two rectangular components like in the picture:
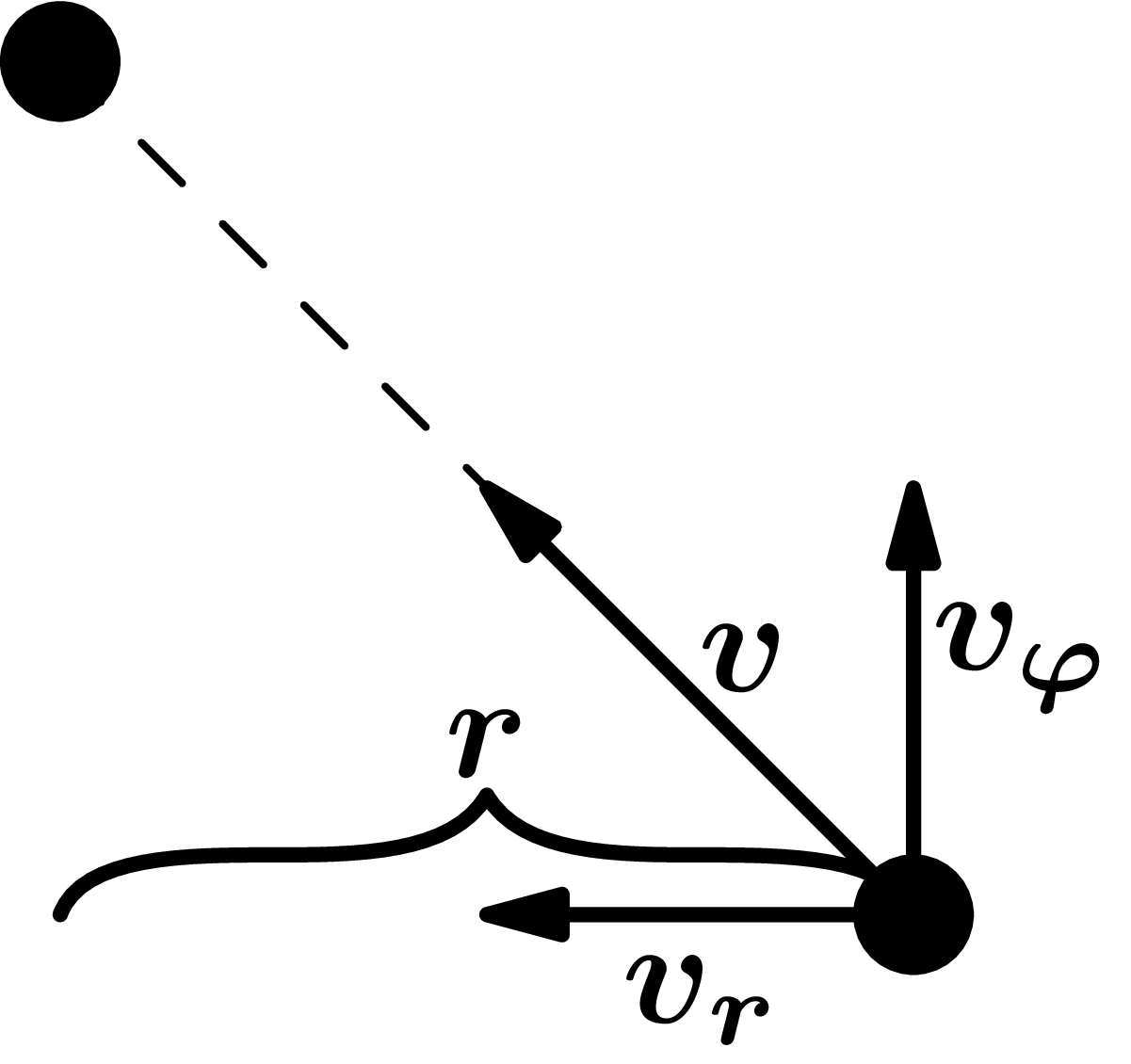
From the geometry of the square, the size of the two speeds is $v\sqrt{2}/2$. The $v_r$ speed is always further in the radius direction. So this is the rate of change in radius, so $$\begin{align*} v_r = -\dot r \,. \end{align*}$$
Minus is here, as the radius wanes. Next, $v_\varphi$ is always perpendicular to $v_r$ and is responsible for changing the angle. This is actually the instantaneous velocity caused by the angular velocity. We can therefore use a relationship $$\begin{align*} v_\varphi = r \dot \varphi = r \omega\,. \end{align*}$$
We got two differential equations that we can solve to figure out the trajectory. The first equation can be solved simply, similar to the case of a falling stone: $$\begin{align*} v_r &= -\dot r \\ \int v_r \, \mathrm{d} t &= -\int \dot r \, \mathrm{d} t\\ r(t) &= C - v_r t \Rightarrow r(t) = (a- v t) \sqrt{2}/2 \,. \end{align*}$$
In integrating $\dot r$, we used the fundamental theorem of differential calculus (integration is, in a sense, the inverse of an operation to a derivative). In the last edit, we just substituted $C= r(0)$, so that the solution matches the initial terms (you can check what $r(0)$) is). Next, we used that $v_r= v\sqrt{2} /2$ and finally we touted a constant.
We can put this solution into the second equation and solve that as well: $$\begin{align*} v_\varphi &= r \dot \varphi = r \omega\\ v_\varphi &= (a- v t) \sqrt{2}/2 \dot \varphi \\ \frac{\sqrt{2} v \sqrt{2}/2}{a- v t} &= \dot \varphi \\ \int \frac{v}{a- v t} \, \mathrm{d}t &= \int \dot \varphi \, \mathrm{d}t\,. \end{align*}$$
We know from experience that the right side will equal the $\varphi$ after integration, the left side is heavier. We can put it back into an integral calculator like WolframAlpha, or we can remember the function logarithm and its derivative. Don't worry about it, if you don't know the logarithm, we'll present it in the next two chapters (you can come back here). Anyway, logarithm is a special function for which: $$\begin{align*} \log'(x) = \frac{1}{x} \,. \end{align*}$$
So we could experiment with different forms of logarithm, and eventually we would find that $$\begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} \left(-\log(a-vt)\right) = \frac{v}{a-vt} \,. \end{align*}$$
You can verify this with the compound function derivative rule, either way we can use it to solve our equation: $$\begin{align*} \int \dot \varphi \, \mathrm{d}t &= \int \frac{v}{a- v t} \, \mathrm{d}t\,. \varphi(t) = -\log(a-vt) + C\,. \end{align*}$$
Constant $C$ We can substitute as $C=\log(r_0)$, which again fulfils the initial conditions, so we get (using the logarithm difference rule): $$\varphi(t) = \log \left( \frac{r_0}{a-vt} \right) \,.$$
The $r$ result confirms our expectations \u2014 the radius linearly wanes with time, and in the predicted time it reaches zero. The angle, on the other hand, changes logarithmically - so the resulting trajectory shape is a logarithmic spiral. This is a magical formation that is, for example, self-similar and perhaps has the shells of a nautilus, the eddies of a tornado, or is the shape of our galaxy. You can see it in the image below.